8кл. География

География 8 класс. Алексеев >>
География 9 класс. Алексеев >>
Физическая география родного края >>

22.11.2022

Тестовое задание
--------------------------
--------------------------

04.10.2022

Урок 10.
РАЙОНИРОВАНИЕ
Макрорегионы России: Западный (Европейская часть) и Восточный (Азиатская часть); их границы и состав. Крупные географические районы России: Европейский Север России и Северо-Запад России, Центральная Россия, Поволжье, Юг Европейской части России, Урал, Сибирь и Дальний Восток.
Практическая работа №3. Обозначение на контурной карте и сравнение границ федеральных округов и макрорегионов с целью выявления состава и особенностей географического положения.

Материалы к уроку


ЦИФРОВЫЕ ОБРАЗОВАТЕЛЬНЫЕ РЕСУРСЫ:

Практическая работа №3. Обозначение на контурной карте и сравнение границ федеральных округов и макрорегионов с целью выявления состава и особенностей географического положения.

Тестовое задание
--------------------------
--------------------------


30.09.2022

Урок 9.

Федеративное устройство России. Субъекты Российской Федерации, их равноправие и разнообразие. Основные виды субъектов Российской Федерации. Федеральные округа. Районирование как метод географических исследований и территориального управления. Виды районирования территории.
Материалы к уроку
*****************
--------------------------
--------------------------


27.09.2022

Урок 8.

Местное, поясное и зональное время: роль в хозяйстве и жизни людей.
Практическая работа №2. "Определение различия во времени для разных городов России и Донецкой Народной Республики по карте часовых зон".
Материалы к уроку
*****************
--------------------------
--------------------------

23.09.2022

Урок 7.

Россия на карте часовых поясов мира.
Карта часовых зон России.
Донецкая Народная Республика на карте часовых поясов.

Материалы к уроку
*****************
--------------------------
--------------------------


20.09.2022

Урок 6.

Ближнее и дальнее зарубежье.
Моря, омывающие территорию России
Материалы к уроку


Моря, омывающие территорию России >>>

Особенности морей,

омывающих территорию России >>>




Моря России >>>

Моря Северного Ледовитого океана >>>

Моря Атлантического океана >>>


Тестовое задание  >>>

********************

**************************************

16.09.2022

Урок 5.

************************

13.09.2022

Урок 4.
Государственная территория России и Донецкой Народной Республики.
Территориальные воды. Государственная граница России и Донецкой Народной Республики.
Морские и сухопутные границы, воздушное пространство, континентальный шельф и исключительная экономическая зона Российской Федерации.
Д/З:
Учить:
Вопросы (с.13) в тетрадь >>>

Тренировочные задания >>>

ЯКЛАСС>>>
Границы Российской Федерации >>>




09.09.2022

*************

02.09.2022

*************


06.05.2022

Растительный и животный мир
России и Донецкого края 


Материалы к уроку

Российская электронная школа: >>>

Урок 18. Растительный мир >>>
Урок 19.Животный мир >>>

Животный мир России >>>

Животные и растения зоны степей >>>

Тестовое задание

ооооооооооооооооо

*****************


06.05.2022

Практическая работа № 8
«Анализ закономерностей распространения почв на территории Донецкого края

04.05.2022

Почвы России и Донецкого края

Учить §§ 21, 22, 23  >>>

Материалы к уроку:

Учить >>>
Учить >>>

Тестовое задание
************************
************************

17.11.2021

Картографические проекции
Картографические проекции карт России и Донецкого края

В современном мире геоинформационные системы позволили создавать электронные географические карты – многослойные, трехмерные, с текстовым и звуковым сопровождением.

- Подумайте, какими геометрическими фигурами можно воспользоваться для изображения шарообразности Земли.

Чтобы правильно изобразить земную поверхность на плоскости, необходимо провести математические расчёты и спроектировать геометрическую фигуру на плоскость, этот процесс называется картографической проекцией.

Картографическая проекция – математический способ перенесения земной поверхности на плоскость карты. Для построения картографической проекции используют вспомогательные геометрические фигуры: цилиндр, конус и плоскость. В зависимости от использования фигуры проекции могут быть цилиндрические, конические и азимутальные.

При составлении цилиндрической проекции используется цилиндр. Такую проекцию чаще всего используют для создания карт мира, материков и океанов, стран, находящихся в приэкваториальной зоне. При использовании такой проекции линии градусной сетки будут пересекаться под прямым углом, меридианы и параллели будут прямыми линиями.

Цилиндрическая проекция










При использовании конуса создается коническая проекция. В этом случае меридианы изображаются прямыми линиями, исходящими из одной точки, а параллели – дугами концентрических окружностей.

При использовании конуса создается коническая проекция. В этом случае меридианы изображаются прямыми линиями, исходящими из одной точки, а параллели – дугами концентрических окружностей.
Коническая проекция
Азимутальную проекцию получают с помощью проектирования картографической сетки Земли на плоскость – касательную к полюсу Земли. Меридианы сетки на проекции имеют вид прямых, исходящих из центральной точки проекции, а параллели – концентрические окружности с центром на полюсе.
Азимутальная проекция

a - цилиндрическая, b - коническая, c - азимутальная, d - псевдоцилиндрическая, 
e - псевдоконическая, f - поликоническая, g - псевдоазимутальная.

Различают проекции нормальные (ось цилиндра или конуса при проецировании совмещена с осью Земли), косые (наклон цилиндра или конуса относительно полярной оси составляет острый угол) и поперечные (угол между осью Земли и осью фигуры проекции составляет 90 градусов). 
При описании проекций много внимания уделяется тому, как выглядят на них параллели и меридианы. Отклонение формы сетки от квадрата показывает степень искажения проецируемого с шара на плоскость изображения. Изучая географическую сетку на карте в какой-либо проекции, можно понять, в какой степени и в каких местах эта карта искажена. 
По типу географической сетки можно выделить: 
- псевдоцилиндрические проекции, у которых параллели - прямые, параллельные друг другу, а меридианы - кривые, симметричные, относительно среднего прямолинейного меридиана; 
- псевдоконические, где параллели - дуги концентрических окружностей, а меридианы - кривые, симметричные относительно среднего прямолинейного меридиана; 
- поликонические, параллели которых - дуги эксцентрических окружностей с центрами на среднем прямолинейном меридиане, а меридианы - кривые, симметричные относительно среднего меридиана. 
На приведенном рисунке видно, какие очертания может принимать географическая сетка в различных проекциях.

Помимо упомянутых, существует много других типов и разновидностей картографических проекций. Проекцию, наиболее подходящую по характеру, величине и распределению искажений для той или иной карты, выбирают в зависимости от назначения, содержания карты, а также от размеров, конфигурации и географического положения поверхности картографируемой территории.

Безусловно, модель нашей планеты удобнее всего представить в виде глобуса, при этом искажения будут минимальны. Однако во время выполнения многих практических и исследовательских задач работать с такой моделью неудобно. Дело даже не в том, что носить с собой глобус не всегда представляется возможным, а в громоздкости такой модели, если мы захотим ее представить в относительно крупном масштабе. Так, если изготовить глобус с изображением поверхности Земли в масштабе 1:1 000 000, то получим шарообразную модель нашей планеты диаметром 12,7 м. Представьте себе, что вам потребуется переносить такую модель, определять на ней координаты точек или производить линейные измерения. По этой причине карты и планы значительно удобнее в пользовании, переноске и хранении.

Геометрические преимущества глобуса (равномасштабность, равноугольность и равновеликость) одновременно и полностью сохранить на плоской карте невозможно. Построенная на плоскости географическая сетка, изображающая меридианы и параллели, будет иметь определенные искажения, поэтому будут искажены изображения всех объектов земной поверхности. Характер и размеры искажений зависят от способа построения картографической сетки, на основе которой составляется карта.

Отображение поверхности эллипсоида или шара на плоскости называется картографической проекцией. По сути, картографическая проекция является горизонтальным приложением точек земной поверхности, расположенных на фигуре Земли. 
Существуют различные виды картографических проекций. Каждому из них соответствуют определенная картографическая сетка и присущие ей искажения. В одном виде проекции искажаются размеры площадей, в другом - углы, в третьем - площади и углы. При этом во всех проекциях без исключения искажаются длины линий.

Выделяют четыре вида искажений на картах: длин, площадей, углов и форм объектов, они видны при сравнении градусной сетки на карте и глобусе.

Вид искажения
 

Определение
 

Признаки на карте
 

Геометрическое выражение
 

На Земле
 

На карте
 

Длин 
 

Одинаковые по длине расстояния на земной поверхности изображены на карте линиями разной длины

Длины равных по величине дуг меридианов на карте разные
 

 



 

 



 

Углов
 

Одноименные углы на земной поверхности и на карте разные

Углы между меридианами и параллелями не прямые

 



 

 



 

Форм
 

Форма географического объекта на земной поверхности и на карте разная
 

1. Отношение длины к ширине объекта на карте отличается от этого же отношения в натуре

2. Клетки сетки на одной широте разной формы

 



 

 



 

Площадей
 

Объекты на земной поверхности с одинаковой площадью изображены на карте участками с разной площадью

Площади клеток картографической сетки на одной широте разные
 

 



 

 
 



По характеру искажений картографические проекции подразделяются на равноугольные(сохраняют углы и формы объектов, но искажают длины и площади); равновеликие(сохраняют площади, но сильно изменяют углы и формы объектов); произвольные(искажения длин, площадей и углов распределены на карте определенным образом),равнопромежуточные (длины сохраняются либо по параллели, либо по меридиану).

Масштаб, указанный на картах, справедлив только на линиях и в точках нулевых искажений. Он называется главным. Во всех остальных частях карты масштаб отличается от главного и называется частным. Для его определения нужны специальные расчеты.

Для перехода от шара (эллипсоида) к плоскости используют специальные вспомогательные поверхности:

цилиндрические (проектирование шара ведется на поверхность цилиндра) - дают наименьшие искажения в области экватора и в средних широтах и используются для построения карт мира;

конические (вспомогательная поверхность - конус) - обладают наименьшими искажениями в умеренных широтах и наиболее точно отражают территорию России;

азимутальные (вспомогательная поверхность - плоскость, которая касается земного шара в одной точке) - обычно используют для отдельных материков.

Поскольку наша планета является геоидом, ее поверхность невозможно перенести на плоскость без неточностей, поэтому все картографические проекции имеют искажения. В зависимости от характера и размера искажений, проекции делятся на равноугольные, равновеликие и произвольные.

Судить о наличии на карте искажения длин удобно путем сравнения величины отрезков меридианов между соседними параллелями. Если они повсеместно равны, то искажения длин по меридианам нет, если такого равенства нет (рис. 5.5 отрезки АВ и CD), то искажение длин линий имеется.

Часть карты восточного полушария с показом картографических искажений

Если карта отображает такую большую территорию, что на ней показаны и экватор 0º и параллель 60° широты, то нетрудно по ней установить, имеется ли искажение длин вдоль параллелей. Для этого достаточно сравнить длину отрезков экватора и параллели с широтой 60° между соседними меридианами. Известно, что параллель 60° широты в два раза короче экватора. Если таково же соотношение указанных отрезков на карте, то искажения длин по параллелям нет; в противном случае оно имеется.
Наибольший показатель искажения длин у данной точки (большая полуось эллипса искажений) обозначают латинской буквой а, а самый меньший (малая полуось эллипса искажений) – b. Взаимно перпендикулярные направления, по которым действуют наибольший и наименьший показатели искажения длин, называют главными направлениями.
В пределах мелкомасштабных карт сравнительно небольших территорий (например, Украины) отклонения масштабов длин от указанного на карте масштаба невелики. Ошибки при измерении длин в этом случае не превышают 2 – 2,5% от измеряемой длины, и ими в работе со школьными картами можно пренебречь. К некоторым картам для приближенных измерений прилагается измерительная масштабная линейка, сопровождаемая пояснительным текстом.

5.2.2. Искажения углов

Искажения углов логически вытекают из искажения длин. За характеристику искажений углов на карте принимают разность углов между направлениями на карте и соответствующими направлениями на поверхности эллипсоида.
За показатель искажения углов между линиями картографической сетки принимают величину отклонения их от 90° и обозначают его греческой буквой ε (эпсилон).
ε = Ө – 90°, (5.8)
где в Ө (тэта) – измеренный на карте угол между меридианом и параллелью.

На рисунке 5.4 обозначено, что угол  Ө равен 115°, следовательно, ε = 25°.
В точке, где угол пересечения меридиана и параллели остается на карте прямым, углы между другими направлениями могут быть измененными на карте, поскольку в каждой данной точке величина искажения углов может изменяться с переменой направления.
За общий показатель искажения углов ω (омега) принимают наибольшее искажение угла в данной точке, равное разности его величины на карте и на поверхности земного эллипсоида (шара). При известных показателях а и b величину ω определяют по формуле:

Искажения площадей

Искажения площадей логически вытекают из искажения длин. За характеристику искажения площадей принимают отклонение площади эллипса искажений от исходной площади на эллипсоиде.
Простой способ выявления искаженности этого вида состоит в сравнении площадей клеток картографической сетки, ограниченных одноименными параллелями: при равенстве площадей клеток искажения нет. Это имеет место, в частности, на карте полушария (рис. 4,4), на которой заштрихованные клетки различаются по форме, но имеют одинаковую площадь.
Показатель искажения площадей (р) вычисляют как произведение наибольшего и наименьшего показателей искажения длин в данном месте карты 
p = а×b (5.10)
Главные направления в данной точке карты могут совпадать с линиями картографической сетки, но могут с ними не совпадать. Тогда показатели а и b по известным m и n вычисляют по формулам:










Входящий в уравнения показатель искажения р узнают в этом случае по произведению:

p = m×n×cos ε, (5.13)

где ε ( эпсилон) – величина отклонения угла пересечения картографической сетки от 90°.

Искажения форм

Искажение форм состоит в том, что форма участка или занятой объектом территории на карте отлична от их формы на уровенной поверхности Земли. Наличие искажения этого вида на карте можно установить путем сопоставления формы клеток картографической сетки, расположенных на одной широте: если они одинаковы, то искажения нет. На рисунке 5.4 две заштрихованные клетки различием формы свидетельствуют о наличии искажения данного вида. Можно также выявить искаженность формы определенного объекта (материка, острова, моря) по соотношению его ширины и длины на анализируемой карте и на глобусе. 
Показатель искажения форм (k) зависит от различия наибольшего (а) и наименьшего (b) показателей искажения длин в данном месте карты и выражается формулой:






При исследовании и при выборе картографической проекции используют изоколы –линии равных искажений. Они могут наноситься на карту в виде пунктирных линий с целью показа величин искажений.
Изоколы наибольших искажений углов










КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ХАРАКТЕРУ ИСКАЖЕНИЙ

Для различных целей создаются различные по характеру искажений проекции. Характер искажений проекции определяется отсутствием в ней определенных искажений (углов, длин, площадей). В зависимости от этого все картографические проекции по характеру искажений подразделяются на четыре группы: 
— равноугольные (конформные); 
— равнопромежуточные (эквидистантные); 
—равновеликие (эквивалентные); 
— произвольные.

Равноугольные проекции

Равноугольными называются такие проекции, в которых направления и углы изображаются без искажений. Углы, измеренные на картах равноугольных проекций, равны соответствующим углам на земной поверхности. Бесконечно малая окружность в этих проекциях всегда остается окружностью.
В равноугольных проекциях масштабы длин в любой точке по всем направлениям одинаковы, поэтому у них нет искажения формы бесконечно малых фигур и нет искажения углов (рис. 5.7, Б). Это общее свойство равноугольных проекций выражает формула ω = 0°. Но формы реальных (конечных) географических объектов, занимающих целые участки на карте, искажаются (рис. 5.8, а). У равноугольных проекций наблюдаются особенно большие искажения площадей (что отчетливо демонстрируют эллипсы искажений).









Вид эллипсов искажений в проекциях равновеликих —- А, равноугольных — Б, произвольных — В, в том числе, равнопромежуточных по меридиану — Г и равнопромежуточных по параллели — Д. На схемах показано искажение угла 45°.

Эти проекции используются для определения направлений и прокладки маршрутов по заданному азимуту, поэтому их всегда используют на топографических и навигационных картах. Недостатком равноугольных проекций является то, что в них сильно искажаются площади рис.а.






















Искажения в цилиндрической проекции:
а –  равноугольной; б – равнопромежуточной; в – равновеликой

Равнопромежуточные проекции

Равнопромежуточными проекциями называют проекции, у которых масштаб длин одного из главных направлений сохраняется (остается неизменным) (рис. Г. рис. Д.) Применяются главным образом для создания мелкомасштабных справочных карт и карт звездного неба.

Равновеликие проекции

Равновеликими называются проекции, в которых нет искажений площадей, т. е. площадь фигуры, измеренной на карте, равна площади этой же фигуры на поверхности Земли. В равновеликих картографических проекциях масштаб площади повсюду имеет одну и ту же величину. Это свойство равновеликих проекций можно выразить формулой:

P = a× b = Const = 1 

Неизбежным следствием равновеликости этих проекций является сильное искажение у них углов и форм, что хорошо поясняют эллипсы искажений (рис. A).

Произвольные проекции

К произвольным относятся проекции, в которых имеются искажения длин, углов и площадей. Необходимость использования произвольных проекций объясняется тем, что при решении некоторых задач возникает необходимость в измерении углов, длин и площадей на одной карте. Но ни одна проекция не может быть одновременно и равноугольной, и равнопромежуточной, и равновеликой. Ранее уже говорилось, что с уменьшением изображаемого участка поверхности Земли на плоскости уменьшаются и искажения изображения. При изображении небольших участков земной поверхности в произвольной проекции величины искажений углов, длин и площадей незначительны, и при решении многих задач их можно не учитывать.

Равноугольные проекции сохраняют без искажений углы и формы малых объектов, зато в них резко деформируются длины и площади. По картам в равноугольных проекциях удобно, например, прокладывать маршруты судов и самолетов, но невозможно измерять площади.

Равновеликие проекции не искажают площадей, но углы и формы объектов в них сильно искажены. Эти проекции хорошо приспособлены для определения площадей (например, размеров государств, земельных угодий).

Произвольные проекции имеют искажения длин, площадей и углов, но они распределяются по карте наиболее выгодным образом. Например, выбирают проекции с минимальными искажениями в центральной части, зато они резко возрастают по краям карты.  произвольные, не сохраняющие ни равенства углов, ни пропорциональности площадей, ни постоянства масштаба. Смысл применения произвольных проекций заключается в более равномерном распределении искажений на карте и удобстве решения некоторых практических задач.

- Проанализируйте физическую карту материков и океанов, какие на ваш взгляд на ней существуют искажения?

- Сравните карту полушарий и карту материков и океанов, найдите примеры искажения фигур и площадей.

Для карт территорий вытянутых по долготе лучшими являются конические проекции. Так, карта Донецкой области выполнена в конической, произвольной проекции, вспомогательной фигурой которой является конус, на картах такой проекции можно измерять углы, расстояния, площади, так как они мало искажены.


С помощью запущенного сервиса «Народная карта», пользователи сети Донецкой области создали карты городов области. Рисунки были сделаны на основании своих знаний и снимков со спутника. На схемах указаны жилые массивы, а также парки, скверы и стадионы. Все созданные карты и схемы будут доступны пользователям Яндекс. Если вам необходим город, а обычной схемы у него нет, при увеличении масштаба, вы увидите схему этого города на Народной карте. На Народной карте можно найти различные достопримечательности того или иного города, а также беседки, обзорные площадки, бюветы, и все это с комментариями и пояснениями. Добавить свою схему на «Яндекс Карты» может любой желающий, достаточно только нарисовать схему на специальном сайте. Руководитель проекта народной карты Павел Гущин заявил, что если каждый человек добавит на карту свой дом, и свою улицу, у всех пользователей появится возможность увидеть подробную и актуальную карту.

Генерализация определяется масштабом карты, ее назначением, тематикой. Наиболее существенно влияет масштаб. Ведь участок местности, которая в реальности имеет площадь 1 км2, на карте масштаба 1:10 000 занимает 1 дм2, На карте масштаба 1:100 000 – 1 см2, А на карте масштаба 1:1000 000 – 1 мм2. Следовательно, все объекты, показанные на карте крупного масштаба, графически невозможно отразить на картах мелких масштабов. А поэтому при переходе к более мелким масштабам, выбирают только самые существенные объекты местности (например, населенные пункты с населением свыше 10 тыс. жителей) и такие, которые могут быть выражены в масштабе этой карты (например, реки длиной более 100 км), упрощают формы объектов (исключают небольшие извилины рек и дорог, выпрямляют контуры береговых линий, границ и т. д.).

На любых географических картах существуют искажения длин, углов, форм и площадей. Эти искажения разных видов, а их величина зависит от вида проекции, масштаба карты и охвата проектируемой территории. Обнаружить на карте искажения длин вдоль меридианов можно, сравнив отрезки меридианов между двумя соседними параллелями – если они находятся на одном уровне, то искажений длины нет. Об искажении расстояний на параллелях свидетельствует соотношение длин отрезков экватора и параллели 60°-й широты между соседними меридианами. Если искажения отсутствуют, то отрезок экватора ровно в два раза больше, чем отрезок 60°-й параллели. О характерном для большинства карт искажении углов можно сделать вывод в том случае, когда параллели и меридианы не образуют между собой прямых углов. Различить искажения формы можно, сравнив длину и ширину какого-либо географического объекта на карте и глобусе – если соотношения форм пропорциональны, то искажения по данному критерию нет. Ещё проще различить искажения формы можно, сравнив ячейки сетки на одной широте: если они одинаковы, то это свидетельствует об отсутствии искажений формы на данной географической карте.

Главное

Карта – это уменьшенное и обобщенное изображение земной поверхности (отдельного участка земной поверхности) на плоскости в масштабе.

Географические карты делятся по масштабу, содержанию, охвату территории, назначению.

Географические карты создают с помощью картографических проекций – математического способа перенесения земной поверхности на плоскость.

В зависимости от искажений картографические проекции могут быть равновеликие, равноугольные, произвольные; в зависимости от вспомогательных фигур: цилиндрические, конические, азимутальные.

Карта Донецкой области создана в конической произвольной проекции.

Вопросы

1. Почему на картах возникают искажения? Какие виды искажений есть на карте часовых поясов мира?

2. Что такое картографическая проекция? Какие их виды вы знаете?

3. Найдите на физической карте Донецкой области примеры различных условных обозначений.

4. Составьте описание любой карты Донецкой области, укажите ее масштаб, элементы содержания.

Задание: Составьте описание любой карты Донецкой области, укажите ее масштаб, элементы содержания.















12.11.2021

Тема: Географические карты. Первая печатная карта Руси.
Виды карт, их классификация. Масштаб. Генерализация.

Домашнее задание - изучить §4 электронного учебника, выписать основные понятия и виды проекций (в тетрадь).

10.11.2021

Местное, поясное время, его роль в хозяйстве и жизни людей

В один и тот же момент в разных точках планеты, лежащих на разных меридианах, будет разное местное (т.е. солнечное) время. Одинаковым время будет только во всех точках, лежащих на одном меридиане, т. е. время обусловлено расположением местности на определенной географической долготе.

Местное время

Измерение времени согласовано со сменой дня и ночи, то есть с вращением Земли вокруг своей оси. Земля осу­ществляет один оборот за сутки, то есть за 24 часа, в каждый час по 15°.

Вращаясь, Земля поворачивается к Солнцу различными меридиа­нами, на которых наступает полдень. В то же время на противополож­ной стороне - полночь. Во всех местах, лежащих на одном меридиане, полдень наступает одновременно, и поэтому они имеют одинаковое местное время.

В прошлом каждый город жил по своему местному време­ни, которое определялось проходящим через него меридианом. Из-за этого возникали большие неудобства в работе железнодо­рожного транспорта и телеграфа. Поэтому было принято единое для всей страны столичное, в России сначала петербургское, а после переноса столицы в Москву - московское время.

Итак, на западных и восточных окраинах даже одного населенного пункта местное время будет отличаться. Эта разница будет нарастать с увеличением расстояния между меридианами. Так, на соседних меридианах, проведенных через 15° разница в местном времени будет составлять 1 час. Проведенных через 1° – 4 мин. Проведенных через 1' (одну минуту) – 4 секунды (именно на такие угловые расстояния вращаются точки одного меридиана за указанные промежутки времени). При этом местное время на меридиане, находящемся восточнее опережает время на меридиане, который находится западнее.

Местное время на меридиане, который находится восточнее от какого-либо пункта, опережает время в нем. Если меридиан лежит западнее, то время отстает. Например, если по местному времени в Киеве полдень (12 ч), то в Донецке уже 12 ч 29 мин. Следовательно, чтобы установить точное время в разных пунктах, зная его в одном из них, нужно осуществить такие вычисления.

1. Найти географическую долготу пунктов:

а) Киев – 30° 34'в. д.;

б) Донецк – 37° 49'в. д.;

2. Установить разницу долгот между пунктами (в градусах и минутах):

между Донецком и Киевом – 37° 49 '- 30° 34' = 7° 15' в. д.;

3. Перевести разницу долгот (с градусов и минут) в разницу во времени (в часы, минуты и секунды): 7°15' = 7° x 4 мин + 15' х 4 с = 29 мин;  найденные величины показывают разницу в местном времени на меридианах, проведенных через Киев и Донецк.

4. К известному нам времени в Киеве (12 ч) нужно прибавить полученную разницу (29 мин) (так как Донецк лежит на восток от Киева):

12 ч + 29 мин = 12 ч 29 мин.

Западная точка области с. Шевченко имеет координаты 47090’ с.ш., 36004’в.д., восточная точка с. Верхний Кут Шахтерского района 47057' с.ш., 39004’в.д., значит, наша область протянулась с запада на восток на 30, то есть разница во времени между западной и восточной точками области будет 12 минут.

Поясное время

Пользоваться местным временем, которое в каждом пункте иное, в повседневной жизни практически невозможно. Для удобства во всем мире пользуются поясным временем. Часовые пояса – регионы Земли, в которых принято одинаковое местное время. Земной шар условно разделен меридианами на 24 полосы (по количеству часов в сутках – на часовые пояса (По 150 долготы каждый – 3600: 24 ч. = 150). В каждом поясе по центру проходит средний меридиан. Местное время этого среднего меридиана договорились считать одинаковым в данный момент для всех пунктов в пределах одного часового пояса. Средние меридианы часовых поясов удалены друг от друга на 150. Границы поясов на морях и океанах проведены прямолинейно по меридианам, на суше для удобства они проведены по государственным и административным границам. Во всех точках одного пояса время одинаковое. Каждому часовому поясу присвоен определенный номер от 0 до 23. Пояс Гринвичского меридиана имеет порядковый номер 0. Время некоторых часовых поясов имеет особые названия. Например, время нулевого пояса называют западноевропейским. Время 1-го пояса – среднеевропейским, время 2-го пояса называют восточноевропейским. Перемещаясь на запад, стрелку часов следует переводить на 1 час назад, если перемещаетесь на восток – на 1 час вперед.

Поясное время легко рассчитать, зная, в каком поясе находится искомый пункт. Например, Москва находится во втором поясе, Калининград в первом, а Киров — в третьем. Разница поясного времени между ними состав­ляет один час.

В России поясное время было введено с 1 июля 1919 г.

Это интересно!

 До введения поясного времени в каждом городе использовалось своё местное солнечное время, зависящее от географической долготы. Система стандартного времени была принята в конце 19 века как попытка покончить с неразберихой, вызванной использованием своего собственного солнечного времени в каждой отдельно взятой местности. Необходимость введения подобного стандарта стала чрезвычайно актуальной с развитием железной дороги, если графики движения поездов составлялись по местному времени каждого города, что вызвало не только неудобства и путаницу, но и частые аварии. Особенно это было актуально для больших территорий, соединенных системой железных дорог. До изобретения железной дороги путешествие из одного места в другое занимало очень много времени. Путешествуя, время нужно было бы переводить лишь на 1 минуту каждые 12 миль. Но после появления железной дороги, с помощью которой стало возможным преодолевать сотни миль в день, расчет времени стал серьезной проблемой. В начале 1880-х годов на Международном астрономическом конгрессе, было принято поясное время, впервые введенное в 1883 году в Канаде и США. В начале ХХ в. поясным временем начали пользоваться в некоторых европейских странах. 

Декретное время

С целью экономии электроэнергии и более эффективного использо­вания светового времени суток в 1930 г. стрелки часов в России были переведены на час вперёд. Так что мы живём по времени сосед­него восточного пояса. Москва, расположенная во втором поясе, живёт по времени третьего пояса, которое называется московским декретным временем. Данное постановление было принято декретом Совета на­родных комиссаров, поэтому называется декретным.

«Летнее» время

Переход на «летнее» время характерен для стран, расположенных в средних широтах, где летнее освещение существен­но отличается от зимнего (рис. 33). Ранний рассвет позволяет раньше начать деловую жизнь без излишнего энергопотребления.

Впервые часовую стрелку перевели в Великобритании в 1908 г. В России переход на «летнее» время первый раз состоялся в 1917 г., с 1981 г. «лет­нее» время начало регулярно действовать - в марте стрелки часов переводятся вперёд. Единственное место в России, где стрелки часов не переводят никогда, - это Центр управления косми­ческими полётами. Круглогодично ЦУП функционирует по так называемо­му декретному московскому времени, соответствующему зимнему. 

 График освещённости на широте Москвы в разное время суток и в разное время года

Линия перемены дат

Рассвет на Землю идёт с востока. Где же начинается новый день? На­чалом суток считают антипод Гринвичского меридиана - меридиан 180°. Он является линией перемены дат, что означает переход из одного дня в другой при её пересечении. Итак, линия перемены дат - это условная линия, по обе стороны от которой часы и минуты совпадают, а календарные даты отличаются на сутки. К западу от линии перемены дат начинается новый день (по календарю). Поэтому в бортовом журнале корабля, который плывет с запада на восток, должны дважды считать один день, а корабль, движущийся с востока на запад, как бы «пропускает» один день, после 31 декабря сразу попадает во 2 января.

Линия перемены дат, как и границы часовых поясов, не полностью совпадает с меридиональным направлением.

Если пересекать линию перемены дат с запада на восток, следует один и тот же день считать дважды, а с востока на запад - пропускать один день.

Это интересно!

Герои романа Жюля Верна «Вокруг света за восемьдесят дней», переезжая в каждый следующий часовой пояс (с запада на восток) переводили стрелки часов на час вперед. В результате, вернувшись в Лондон, они как бы «приобрели» целые сутки, так как не учли линию перемены дат, на которой нужно было вернуться в предыдущие сутки.

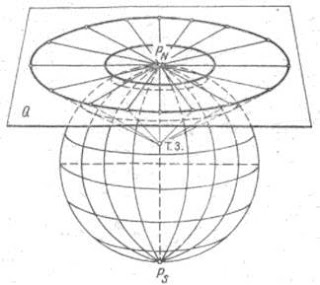
 На Северном и Южном полюсах меридианы сходятся в одной точке, и поэтому там понятие часовых поясов, а заодно и местного времени, теряет смысл. Считается, на полюсах должно использоваться всемирное время, однако на станции Амундсен-Скотт (Южный полюс) действует время Новой Зеландии.

Согласованность времени в разных регионах огромной России - условие величайшей важности для создания единого экономического простран­ства. Организация часовых поясов позволила упорядочить местное время и выделить часовые пояса.


Письменно в тетрадях:

1.     - Почему необходим был переход от местного к поясному времени?

2.     - В каких часовых поясах располагается наша страна?

3.     - Чем вызван переход на декретное и «летнее» время?

4.     - Что такое линия перемены дат?

5.     - Где проходит линия перемены дат?

6.     - Как можно «найти» или «потерять» одни сутки?

Проработать §3 сс.14-18 параграф в учебнике.

Пользуясь картой часовых поясов, выполните задания:

7.     Определите местное время в Донецке, если на нулевом меридиане местное время составляет 16.00 ч.

8.     Солнечное время в Донецке 13.00. Определите, на котором меридиане в этот момент будет 17.00.

9.     Определите географическую долготу пункта А, если на нем местное время 10 ч 30 мин, а в Лондоне 8 ч.

10.  Составьте задачу на определение поясного времени.



Комментарии

Отправить комментарий